Odd number theorem

The odd number theorem is a theorem in strong gravitational lensing which comes directly from differential topology. It says that the number of multiple images produced by a bounded transparent lens must be odd.

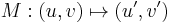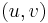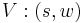In fact, the gravitational lensing is a mapping from image plane to source plane M: (u,v) \mapsto (u',v')\,. If we use direction cosines describing the bended light rays, we can write a vector field on (u,v)\, plane V:(s,w)\,. However, only in some specific directions 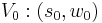V_0:(s_0,w_0)\,, the bended light rays will reach the observer, i.e., the images only forms where 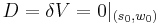D=\delta V=0|_{(s_0,w_0)}. Then we can directly apply Poincaré–Hopf theorem 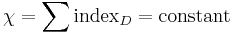\chi=\sum \text{index}_D = \text{constant}\,. The index of sources and sinks is +1, and that of saddle points is −1. So the Euler characteristic equals the difference between the number of positive indice 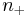n_{%2B}\, and the number of negative indice 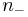n_{-}\,. For the far field case, there is only one image, i.e., 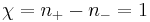\chi=n_{%2B}-n_{-}=1\,. So the total number of images is 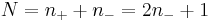N=n_{%2B}%2Bn_{-}=2n_{-}%2B1 \,, i.e., odd. The strict proof needs Uhlenbeck’s Morse theory of null geodesics.

References